Поворотная гомотетия. Часть I
Что такое поворотная гомотетия?
Поворотная гомотетия это, как следует из названия, композиция поворота и гомотетии. Удобно смотреть на это с точки зрения векторов на плоскости: при повороте все векторы поворачиваются на один и тот же угол, а при гомотетии растягиваются в одно и то же количество раз. При поворотной гомотетии все векторы поворачиваются и растягиваются, при этом и угол поворота, и коэффициент растяжения у всех векторов одинаковый. Это, в частности, означает, что поворотная гомотетия переводит фигуры в подобные, прямые — в прямые, окружности — в окружности, сохраняя в процессе всевозможные пропорции.
Оказывается у поворотной гомотетии (если она не тривиальная, то есть угол поворота не кратен \(360^\circ\), а коэффициент растяжения не равен 1) обязательно есть неподвижная точка, называемая центром поворотной гомотетии. Центр легко построить по любой точке \(A\) и ее образу \(A'\) — достаточно лишь найти такую точку \(O\), что угол \(AOA'\) равен углу поворота, а отношение \(A'O/AO\) равно коэффициенту растяжения.
Отмечу, что коэффициент растяжения у поворотной гомотетии может быть и отрицательным (как у обычной гомотетии), однако этого можно легко избежать, добавив при необходимости к углу поворота \(180^\circ\) (поворот на развернутый угол является центральной симметрией). Композиция поворотных гомотетий, согласно определению, почти всегда является поворотной гомотетией. Исключение составляют лишь те случаи, когда сумма углов поворотов кратна \(360^\circ\), а произведение коэффициентов равно 1. В этом случае все векторы в результате выполнения композиции сохраняют свои направления и длины, то есть композиция является параллельным переносом.
Как совместить поворотной гомотетией два отрезка?
Предположим, что на плоскости даны два отрезка \(AB\) и \(A'B'\) и мы хотим совместить их поворотной гомотетией так, что бы точка \(A\) перешла в точку \(A'\), а точка \(B\) — в точку \(B'\). Всегда ли это можно сделать? Единственным ли способом? Как найти центр соответствующей поворотной гомотетии?
Есть пара тривиальных случаев. Если отрезки равны и параллельны, то совместить их поворотной гомотетией, конечно, нельзя — роль нужной поворотной гомотетии в этом случае выполняет параллельный перенос. Если отрезки параллельны, но не равны, то очевидно, что можно обойтись обычной гомотетией с центром в точке \(O\) пересечения прямых \(AA'\) и \(BB'\) (треугольники \(OAB\) и \(OA'B'\) в этой конфигурации подобны в виду параллельности прямых \(AB\) и \(A'B'\)).
Перейдем теперь к общему случаю. Пусть отрезки \(AB\) и \(A'B'\) не параллельны, тогда легко определить угол поворотной гомотетии — он в точности равен углу между отрезками (тут правильно было бы говорить ``направленному углу’’). То есть если прямые \(AB\) и \(A'B'\) пересекаются в точке \(X\), то центр поворотной гомотетии \(O\) должен удовлетворять равенствам \[ \angle AOA'=\angle BOB'=\angle AXA'=\angle BXB'. \] Опять же равенство надо воспринимать как равенство направленных углов. Это означает, что центр поворотной гомотетии должен лежать одновременно на описанных окружностях треугольников \(AXA'\) и \(BXB'\). Одна точка пересечения окружностей это точка \(X\). Она годится в качестве центра только в случае подобия треугольников \(XAA'\) и \(XBB'\), то есть в случае параллельности прямых \(AA'\) и \(BB'\) и касания описанных окружностей треугольников \(AXA'\) и \(BXB'\), то есть по сути когда вторая точка пересечения \(O\) совпадает с точкой \(X\).
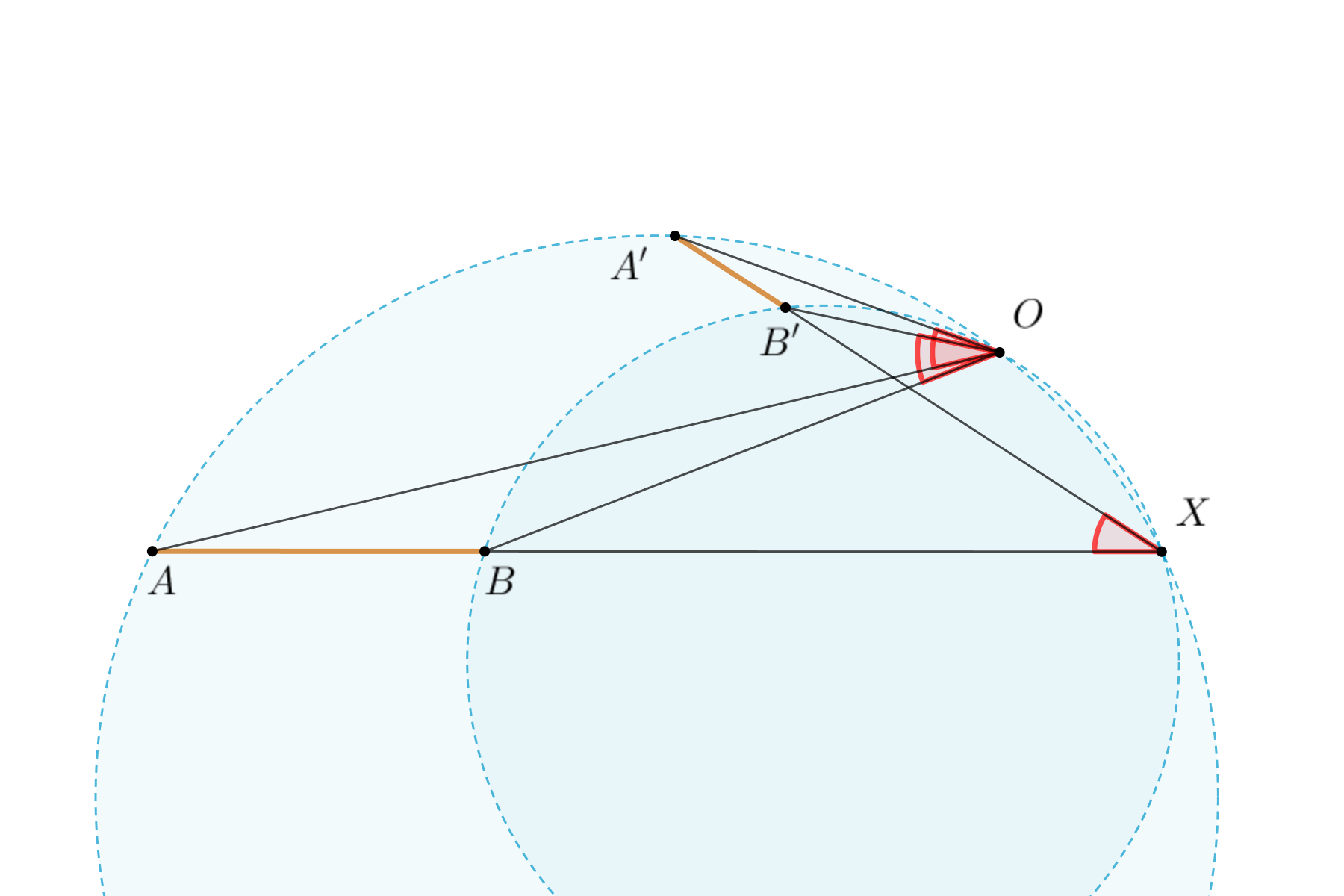
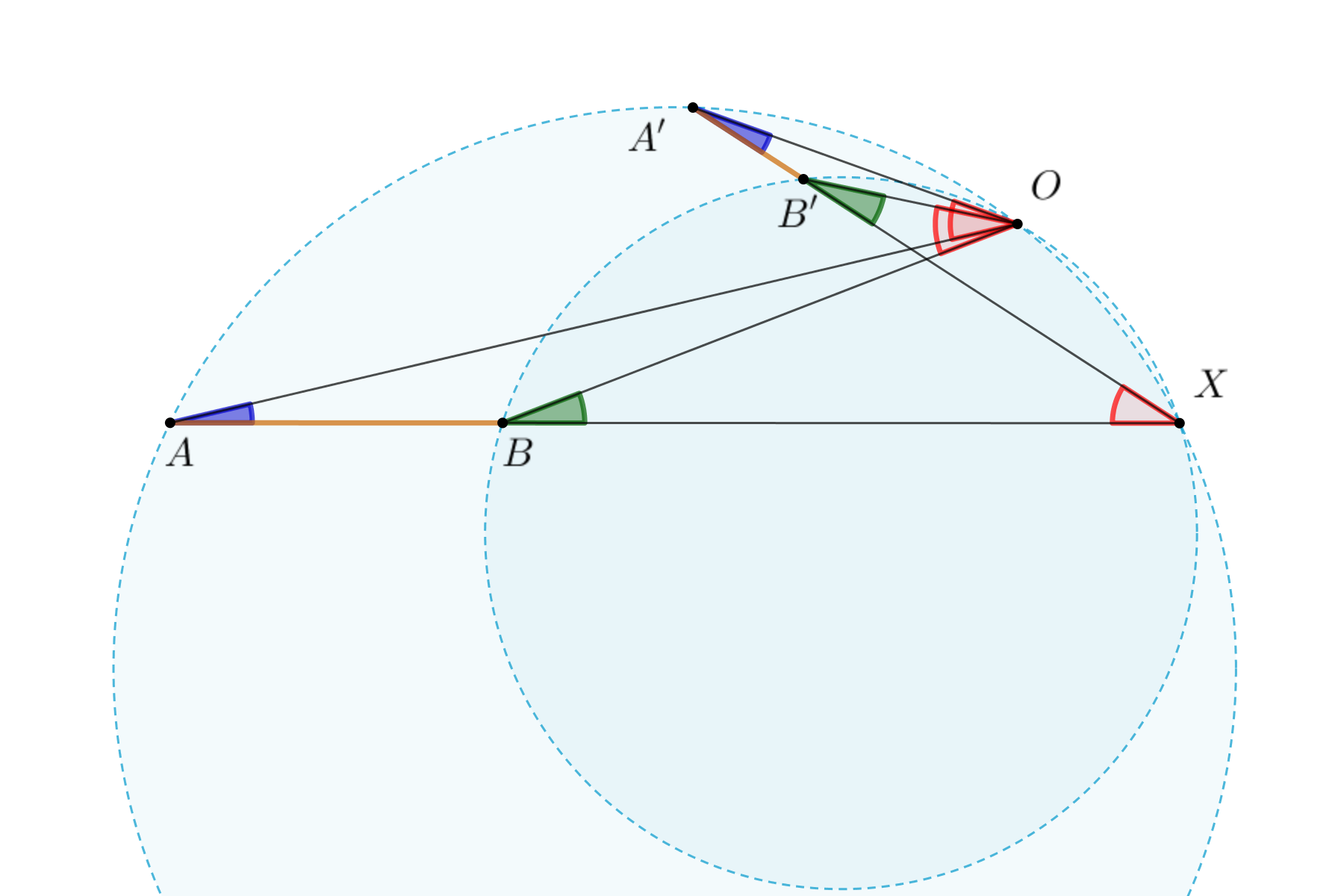
Центр поворотной гомотетии найден, он существует всегда, кроме вырожденной ситуации, единственен и может быть найден как точка пересечения двух окружностей. Круто!
Важное наблюдение и точка Микеля
Самое поразительное и простое наблюдение, которое можно сделать состоит в том, что если \(O\) — центр поворотной гомотетии, переводящей отрезок \(AB\) в отрезок \(A'B'\), то точка \(O\) является и центром поворотной гомотетии, переводящей отрезок \(AA'\) в отрезок \(BB'\). Действительно, из подобия треугольников \(OAB\) и \(OA'B'\) легко вывести подобие треугольников \(OAA'\) и \(OBB'\), сравнив углы и отношения отрезков с вершиной \(O\).
Но мы же знаем как строится центр поворотной гомотетии, переводящей отрезок \(AA'\) в отрезок \(BB'\) в случае их непараллельности — надо пересечь прямые \(AA'\) и \(BB'\) в точке \(X'\) и вторая точка пересечения окружностей, описанных около треугольников \(ABY\) и \(A'B'X'\), и будет центром поворотной гомотетии.
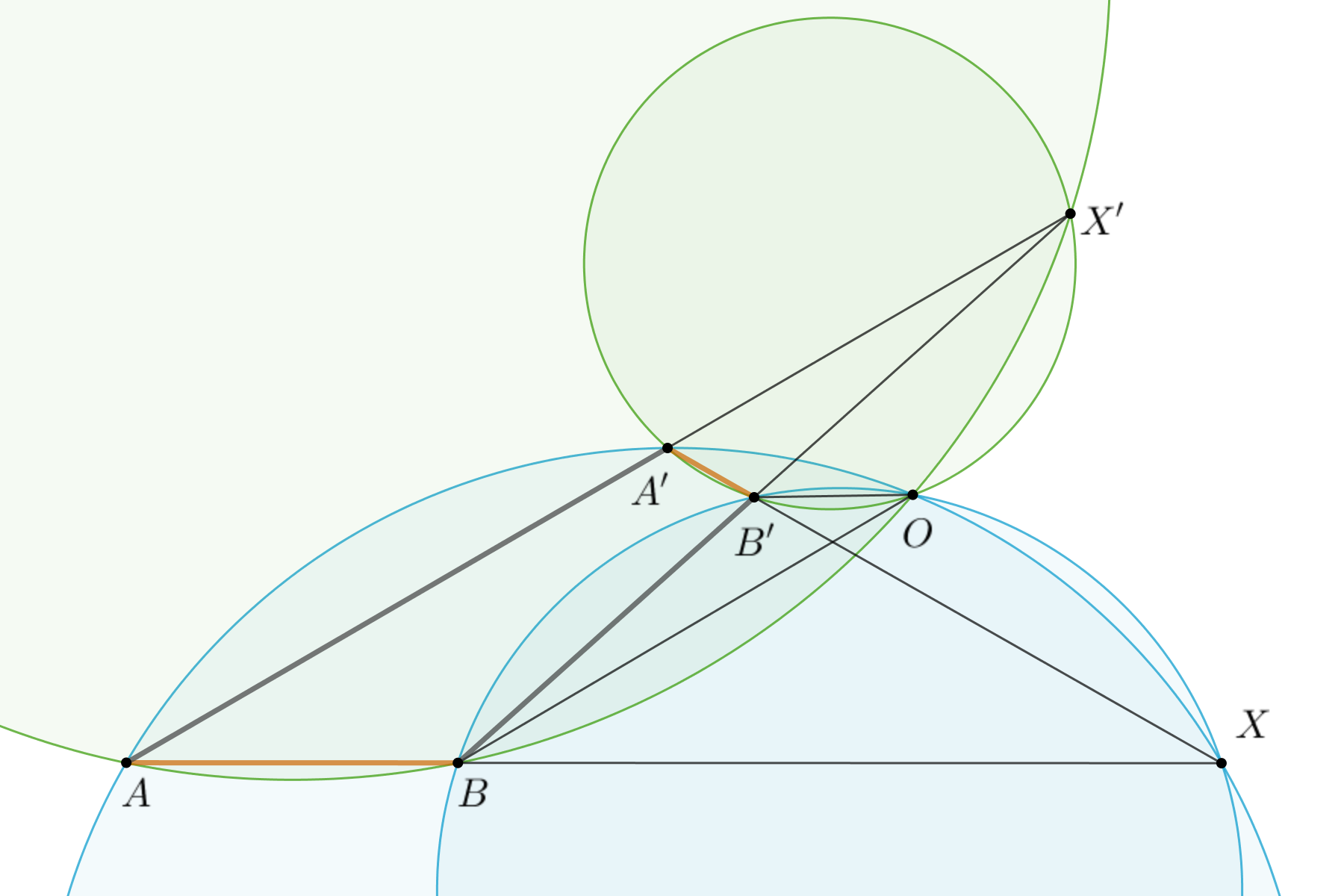
Какой вывод можно сделать? Сразу четыре окружности проходят через одну точку: окружности, описанные около треугольников \(AA'X\), \(BB'X\), \(ABX'\) и \(A'B'X'\). Это утверждение можно сформулировать следующим образом.
Точка Микеля.
Для любых четырех прямых описанные окружности четырех образуемых ими треугольников пересекаются в одной точке. Эта точка называется точкой Микеля четырех прямых.
Подробнее говорить о точке Микеля в этой статье мы не будем. Отмечу только, что это очень сильное утверждение, которое, при должном умении и правильном восприятии, позволяет в различных задачах многое сразу видеть на геометрической картинке. Если вы никогда этого утверждения не видели, попробуйте с его помощью доказать факт о прямой Симсона: основания перпендикуляров из точки \(P\) на стороны треугольника \(ABC\) лежат на одной прямой тогда и только тогда, когда точка \(P\) попадает на описанную окружность треугольника \(ABC\).